How To Find The Slope Of A Tangent Line Without Using Derivatives

In terms of the W function, which was developed specifically to solve equations of this type. While there does exist a general algebraic method for computing derivatives, there is no general algebraic method for solving equations. Even for polynomials, it is known that there can be no generally useful algebraic method of finding roots (i.e., there can be no analog of the quadratic formula) for degree five or above. This is why it is often necessary to resort to numerical approximation methods to solve algebraic equations.

The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.

The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. You can determine the slope of a tangent line at any point on a function using calculus. The calculus approach requires taking the derivative of the function from which the tangent line originates. By definition, the derivative of a function at any given point is equal to the slope of the tangent at that point.

This value is also sometimes described as the instantaneous rate of change of the function. Although calculus has a reputation for being difficult, you can find the derivative to most simple algebraic functions quickly. Together we will walk through three examples and learn how to use the point-slope form to write the equation of tangent lines and normal lines. In mathematics, slopes and tangents help determine ratios and rates of change.

Learn how to show slopes and tangents as lines on a graph, explore the concept of slope as it pertains to hills, and recognize how slope can be used to describe steepness. The tangent line of a curve at a given point is a line that just touches the curve at that point. The tangent line in calculus may touch the curve at any other point and it also may cross the graph at some other point as well. If a line passes through two points of the curve but it doesn't touch the curve at either of the points then it is NOT a tangent line of the curve at each of the two points. Here, we can see some examples of tangent lines and secant lines.

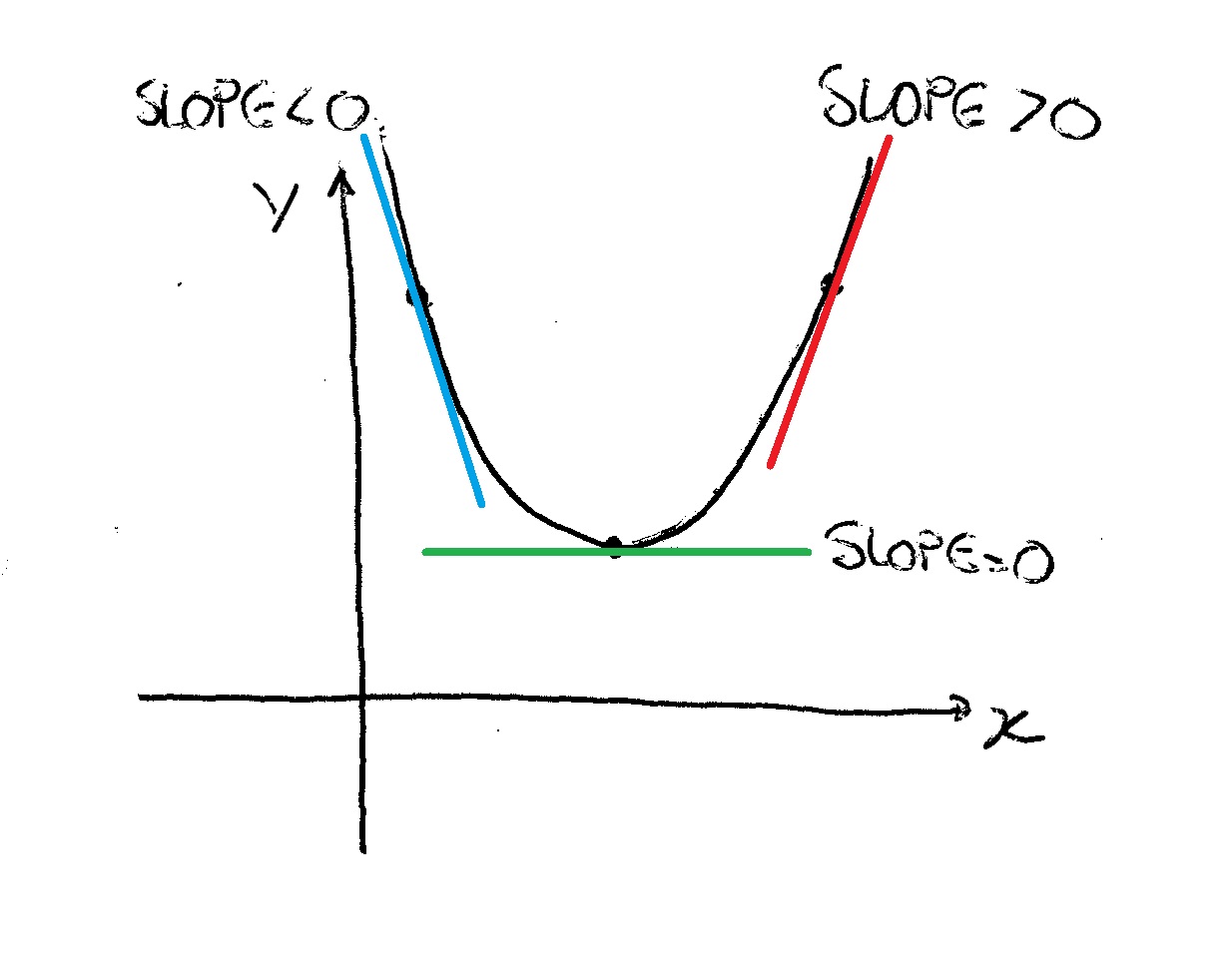
The problem of finding the slope of the tangent line to a curve and the problem of finding the instantaneous velocity of an object both involve finding the same type of limit. A horizontal tangent is parallel to x-axis and hence its slope is zero. We know that the slope is nothing but the derivative of the function. So to find the points where there are horizontal tangents just set the derivative of the function to zero and solve. After getting the points, we can find the equation of the horizontal tangent line using the point-slope form.

The derivative of a function is interpreted as the slope of the tangent line to the curve of the function at a certain given point. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′.

For any constant C, we see that all the tangent line segments along this line have the same slope, no matter what the value of the independent variable, say t. Another way to look at this is to realize that we can generate infinitely many solutions by taking any one solution and translating its graph left or right. Even when we can't solve an equation, an analysis of its slope field can be very instructive. However, such a graphical analysis may miss certain important features of the integral curves, such as vertical asymptotes. Many common questions asked on the AP Calculus Exams involve finding the equation of a line tangent to a curve at a point. If we are adept at quickly taking derivatives of functions, then 90 percent of the work for these types of problems is done.

Likewise, we can even extend this concept to writing equations of normal lines, which are also called perpendicular lines. The only difference will be that we will simply use the negative reciprocal slope of the line tangent. Therefore, let's formally lay out the steps for writing the tangent line equation to a curve, as this particular skill is pivotal for future lessons dealing with linearization and differentials. Separable differential equations are used to rearrange variables so that all terms of one variable are on one side of the equation, thus ''separating'' the variables.

See the steps involved in recognizing and solving these types of differential equations. When studying mathematics functions and methodology of calculation, a good place to start is understanding the significance of one-sided limits and continuity. Learn more about the properties and functions, and study an example of a formula for finding one-sided limits and continuity. A vertical tangent is parallel to y-axis and hence its slope is undefined. As the slope is nothing but the derivative of the function, to find the points where there are vertical tangents, see where the derivative of the function becomes undefined . After getting the points, we can find the equation of the vertical tangent line using the point-slope form.

The "tangent line" is one of the most important applications of differentiation. The word "tangent" comes from the Latin word "tangere" which means "to touch". The tangent line touches the curve at a point on the curve. So to find the tangent line equation, we need to know the equation of the curve and the point at which the tangent is drawn.

The point at which the tangent is drawn is known as the "point of tangency". The intuitive notion that a tangent line "touches" a curve can be made more explicit by considering the sequence of straight lines passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope.

Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation.

This result is the equation of the tangent line to the given function at the given point. When we have a function that isn't defined explicitly for ??? Consequently, when we define the derivative as the slope of the tangent, we fail to convey the meaning that makes the derivative so useful. If we want students to understand this meaning, the derivative must be introduced in terms of a multiplicative relationship between changes in the variables. It must be grounded in a thorough understanding of what average rates of change tell us and what a constant rate of change actually implies. The belief that average rates of change are not significant is reinforced when, as in Stewart's calculus, the derivative is introduced as the slope of the tangent line.

The problem is thatslopeis a problematic concept for many students. Identifying the derivative with the slope of a tangent line suggests a geometric understanding of derivatives. But too often it does no such thing, instead short-circuiting student development of an understanding of the derivative as describing the multiplicative relationship between changes in two linked variables. As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change. So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement.

Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change. I always like solving advanced problems with basic methods. For example, many problems that we usually think of as "algebra problems" can be solved by creative thinking without algebra; and some "calculus problems" can be solved using only algebra or geometry. Using simple tools for a big job requires more thought than using "the right tool", but that's not a bad thing.

I want to look at several ways to find tangents to a parabola without using the derivative, the calculus tool that normally handles this task. Calculus equations that seek to determine the maximum or minimum value for a given parameter are called optimization problems. Learn about optimization problems through real-world examples/explanations and how to use the six-step method to solve optimization problems in calculus. Next, let's find the equations of the lines that are normal to the curve at these two points. To write the equation of a line, we need to know its slope, and one point on the line.

A cusp corresponds to a "corner" or abrupt change in direction of a curve representing a function that is continuous at the point in question. The curve has different tangents immediately to the right and left of a cusp. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz. Differentiate the equation of the circle and plug in the values of x,y in the derivative.

Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. Also, do not worry about how I got the exact or approximate slopes. We'll be computing the approximate slopes shortly and we'll be able to compute the exact slope in a few sections.

For a general curve, finding the tangent line is also done by finding the solutions to two equations in two unknowns found in a similar manner as above. However, it might require the use of 'fzero' or even 'fsolve' to find the solutions, depending on the nature of the curve's equation. These two equations lead to a simple quadratic equation in x which has either two solutions, one solution, or none, depending on , and therefore a similar number of possible tangent lines.

The fundamental theorem of calculus allows us to calculate indefinite integrals as the anti-derivatives of the original polynomial function. Learn how to calculate indefinite integrals of polynomials through several examples and how to apply a general rule to polynomials with any number of variables. Let us see how to find the slope and equation of the tangent line along with a few solved examples. Also, let us see the steps to find the equation of the tangent line of a parametric curve and a polar curve. Differentiation of algebraic and trigonometric expressions can be used for calculating rates of change, stationary points and their nature, or the gradient and equation of a tangent to a curve.

The derivative of a function has many applications to problems in calculus. It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values. In the differential equations and dynamic optimization, where the independent variable is the time. At the point P means the slope of the tangent at the point P.

We need to find this slope to solve many applications since it tells us the rate of change at a particular instant. Drag the red point to see how the tangent changes along the curve. Drag the green point to see how the secant line approaches the tangent as the green dot approaches the red dot . Not also how each of the slopes of the tangent and secant lines change . Many calculus books will treat this as its own problem.

We however, like to think of this as a special case of the rate of change problem. In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\). Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing. Because if we are ever asked to solve problems involving the slope of a tangent line, all we need are the same skills we learned back in algebra for writing equations of lines. Find the equation of the line that is tangent to the curve at the point $(0,\sqrt)$. Finding tangent line equations using the formal definition of a limit This is the currently selected item.

Sometimes function is defined parametrically, but we still need to find equation of tangent line. The slope of the line tangent in the point P1 will be the arithmetic mean of the slopes of the two secant lines. This method of calculation is possible because we have chosen the x0 and x2 points at equal distance from x1. We could estimate the slope of L from the graph, but we won't. Instead, we will use the idea that secant lines over tiny intervals approximate the tangent line. Use a derivative and perpendicular slope of a tangent line to calculate the equation of the normal line.

When looking at a graph, the concavity of a function is determined by the changes to its derivative. Learn how to define concavity and inflection points with differentiation by going over a review of concavity and four concavity examples. Learn what a derivative of a function is, the notational definition of a derivative formula, what higher-order derivatives are, and see worked-out examples. Learn how to find a tangent line, and how to write the equation of a tangent line. You can do this for any differentiable function, and can use derivative approximation methods to eliminate the need to provide the analytical derivative. Our final answer is the two equations with the green checkmarks next to them, and we've plotted those two lines, and the orignal function's curve, on the lower graph below.

BUT, much more important is the process we used to find those equations, and we hope that makes sense. Rather than ignoring the relationship between the two points, as in the first form, this formula relies upon it. The major difference here, though, is that x2 has been replaced by the first x plus some change "h". The slope formula's premise still stands, however, as the new form does in fact calculate change in y over change in x. What we want is a line tangent to the function at (1, 1/2) -- one that has a slope equal to that of the function at (1, 1/2).

Give the diagram of the given function, of the tangent line equation and the numerical versus exact derivative. We will now extend this numerical approach so that we can find the slope of any continuous curve if we know the function. We will learn about an algebraic approach that can be used for most functions. The problematic nature of slope and rates of change was nicely documented in a paper by Cameron Byerley and Pat Thompson that appeared last year in theJournal of Mathematical Behavior. In the summers of 2013 and 2014, they administered a diagnostic instrument requiring written responses to 251 high school mathematics teachers. In reality there probably won't be 15 cm3 more air in the balloon after an hour.

The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour. In other words, as we take \(Q\) closer and closer to \(P\) the slope of the secant line connecting \(Q\) and \(P\) should be getting closer and closer to the slope of the tangent line. If you are viewing this on the web, the image below shows this process.

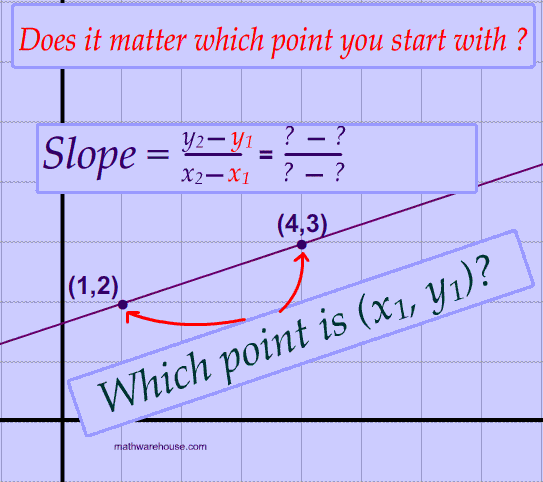
Having two points defined we can easily draw a straight line between them. Also with the coordinates of the two points we can calculate the slope of the line. Given a function f and a point P1, how do we calculate the tangent?